| |
  |
 |
 |
Mean Polynomial Kernel |
| |
Classification tasks in computer vision and braincomputer interface research have presented several applications such as biometrics and cognitive training. However, like in any other discipline, determining suitable representation of data has been challenging, and recent approaches have deviated from the familiar form of one vector for each data sample. This paper considers a kernel between vector sets, the mean polynomial kernel, motivated by recent studies where data are approximated by linear subspaces, in particular, methods that were formulated on Grassmann manifolds. This kernel takes a more general approach given that it can also support input data that can be modeled as a vector sequence, and not necessarily requiring it to be a linear subspace. We discuss how the kernel can be associated with the Projection kernel, a Grassmann kernel. Experimental results using face image sequences and physiological signal data show that the mean polynomial kernel surpasses existing subspace-based methods on Grassmann manifolds in terms of predictive performance and efficiency.
|
|
| |
|
|
| |
 |
|
| |
 |
|
| |
 |
|
| |
 |
|
| |
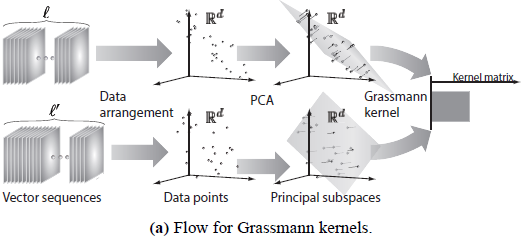
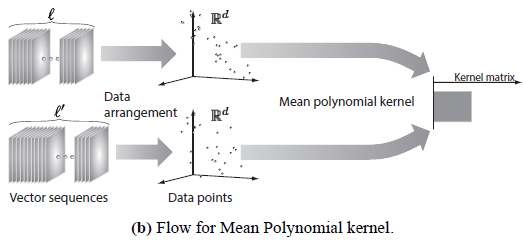
Fig. 3 Flow of methodology for computing values for Grassmann kernels and the mean polynomial kernel. Grassmann kernels are defined on a Grassmann
manifold which is a set of linear subspaces. When employing these kernels, each vector sequence, represented by a set of data points on space, is approximated
by a principal subspace obtained via PCA. However, this poses a threat of some degree of information loss, and is more likely to consume more time due to
eigendecomposition. The mean polynomial kernel, on the other hand, can be directly applied to compute the kernel value between the sets of data points. It
can avoid information loss while being more time efficient. |
|
| |
|
|
| |
References |
|
| |
Raissa Relator, Yoshihiro Hirohashi, Eisuke Ito, Tsuyoshi Kato, Mean Polynomial Kernel and Its Application to Vector Sequence Recognition, IEICE Transactions on Information & Systems,Vol.E97-D,No.7,pp.1855-1863, Jul. 2014. |
|
| |
Raissa Relator, Yoshihiro Hirohashi, Tsuyoshi Kato,
Mean polynomial kernel for face membership authentication.
MVA 2013,Oral Presentation in Ritsumeikan University. |
|
| |
|
|
| |
|
|
| |
|
|
|
|
|
|
