| |
  |
 |
 |
 |
| |
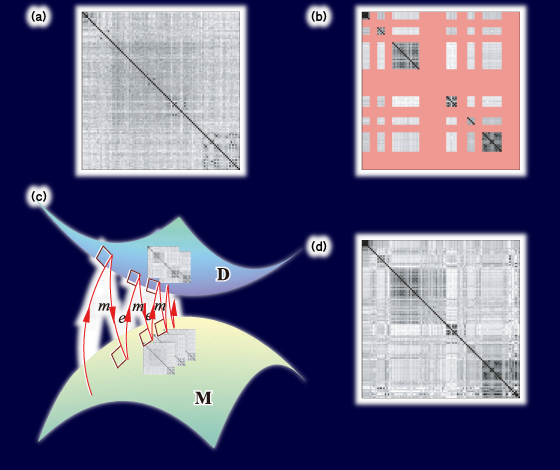
タンパク質の表現として,立体構造とアミノ酸配列があります.タンパク質の機能は立体構造から決まります.したがって,特定のタンパク質の機能を予測するには,機能既知のタンパク質の立体構造と調べたいタンパク質の立体構造をカーネル法などの機械学習法を使って比較すればよいことになります.タンパク質の立体構造を実験的に同定するには,多くの費用と時間を要します.それに対して,アミノ酸配列は容易に手に入れることができますが,アミノ酸配列から機能を予測するのは難しいタスクです.そこで,アミノ酸配列のカーネル行列(類似度行列のようなもの)と立体構造のカーネル行列の一部を使って,立体構造のカーネル行列の残りの部分を推定する算法を開発しました.(a)がアミノ酸配列から得られたカーネル行列,(b)がタンパク質立体構造から得られたカーネル行列列です.赤い部分は立体構造がなかったため欠損しています.これを配列のカーネル行列を使って欠損を埋めます.幾何学的には(c)に示すように,立体構造カーネルと配列カーネルの多様体を考え,距離が最小になる地点を探します.この方法により補完された立体構造カーネルを(d)に示します. |
|
| |
|
|
| |
 |
|
| |
図 (a)アミノ酸配列から得られたカーネル行列,(b)がタンパク質立体構造から得られた不完全カーネル行列,(d)em法,(d)補完した行列. |
|
| |
|
|
| |
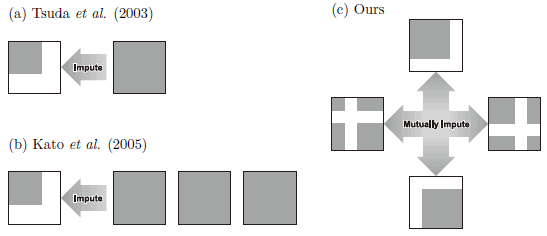
さらに,下図(c)のようにカーネル行列間を相互に補完する方法も開発した. |
|
| |
|
|
| |
 |
|
| |
|
|
| |
文献 |
|
| |
[2] Tsuyoshi Kato, Taishin Kin, Kentaro Tomii, Koji Tsuda, Kiyoshi Asai:
A kernel-based approach for estimating structural similarities from sequences,
CBRC Technical Report, AIST02-J00001-3, pp.1--19, Jan. 20, 2004. |
|
| |
[3] Taishin Kin, Tsuyoshi Kato and Koji Tsuda:
Protein Classification via Kernel Matrix Completion,
(Eds.) Schoelkopf, B., K. Tsuda and J.P. Vert , Kernel Methods in Computational Biology, pp.261--274, 2004 |
|
| |
Rachelle Rivero, Richard Lemence, Tsuyoshi Kato,
Mutual Kernel Matrix Completion, IEICE Transactions on Information & Systems,
Vol.E101-D,No.8,pp.-,Aug. 2017. |
|
| |
Rachelle Rivero, Tsuyoshi Kato, Parametric Models for Mutual Kernel Matrix Completion, IEICE Transactions on Information & Systems, Vol.E101-D,No.12,pp.-,Dec. 2018. doi: 10.1587/transinf.2018EDP7139 |
|
|
|
|
|
